[Paper Review] Time Series Forecasting With Deep Learning: A Survey

Paper Information

Title: Time Series Forecasting With Deep Learning: A Survey Authors: Bryan Lim, Stefan Zohren Link: https://arxiv.org/abs/2004.13408

Summary

• 본 논문에서 저자들은 CNN-based Encoder, RNN-based Encoder, Attention-based Encoder에 대한 간단한 설명을 제시하였다.
• 또한 심층 신경망 모델을 Point Estimates와 Probabilistic Output으로 나누어 그 차이에 대해 설명하였으며, 도메인 지식과 합쳐진 Hybrid model에 대해 간단한 설명을 추가하였다,.
• 저자들은 데이터가 복잡해지고 커지는 현재 사용자들이 데이터간 관계를 제대로 파악하기 어렵다고 생각하였으며, 설명 가능한 AI (XAI)의 필요성을 언급하였다.
• 또한, 기존 딥러닝 모델들은 데이터를 일정한 간격으로 이산화해야 하므로 관측치가 누락되거나 임의의 간격으로 도착할 수 있는 데이터 셋을 예측하는데 어려움있다는 점을 한계점으로 제시하였으며 이에 대한 추가적인 연구가 필요하다고 제시하였다.

Introduction

• Autoregressive (AR), Exponential Smoothing, Structual Time Series Model과 같은 전통적인 기법들은 도메인 지식을 기반으로 한 모수적 모델 (Parameteric model)에 초점을 맞추고 있다.
• 머신러닝을 기반으로 한 최근 기법들은 도메인 지식 없이 순수하게 데이터 적 측면에서 시간적 역학(Temporal Dynamics)을 학습하는 수단을 제공한다.

Deep Learning Architectures for Time Series Forecasting

Single-step Time Series Forecasting을 수식으로 나타내면 아래와 같다.

\[\hat{y}_{i,t+1}=f(y_{i,t-k:t},\boldsymbol{x}_{i,t-k:t},\boldsymbol{s}_{i})\]

수식에서 \(\hat{y}_{i,t+1}\)는 이어지는 다음 스텝의 $i$-번째 타겟에 대한 예측을 의미하며, \(y_{i,t-k:t}\)와 \(\boldsymbol{x}_{i,t-k:t}\)는 예측에 활용되는 이전 \(k\) 스텝의 관측치와 특징들을 의미한다. \(\boldsymbol{s}_{i}\)는 각 개체와 관련된 정적인 메타데이터이다.

(a) Basic Building Blocks

저자들은 시계열 분석을 입력 특징들을 latent variable \(\boldsymbol{z}_t\)로 인코딩하고, \(\boldsymbol{z}_t\)를 활용하여 최종 예측을 진행하는 관점으로 고려하였으며, 위 수식을 아래와 같이 다시 나타냈다.

\[\begin{align} f(y_{t-k:t}, \boldsymbol{x}_{t-k:t}, \boldsymbol{s}) &= g_{dec}(\boldsymbol{z}_{t}),\\ \boldsymbol{z}_{t} &= g_{enc}(y_{t-k:t},\boldsymbol{x}_{t-k:t}, \boldsymbol{s}) \end{align}\]

본 논문에서는 편의를 위해 수식에서 변수 인덱스 \(i\)를 생략했다. (즉, \(y_{i,t}\)는 \(y_{t}\)로 대체되었다.) 또한, \(g_{enc}(\cdot)\)과 \(g_{dec}(\cdot)\)는 각각 인코더(Encoder)와 디코더(Decoder) 함수를 의미한다.

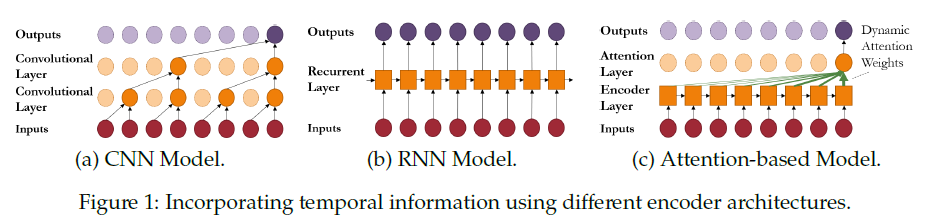
저자들은 Figure 1을 통해 기본적인 인코더 구조 (CNN 모델, RNN 모델, Attention 기반의 모델)를 보여주었으며 이어지는 파트를 통해 전통적인 시계열 모델간의 관계에 대해 설명하였다.

(i) Convolutional Neural Networks

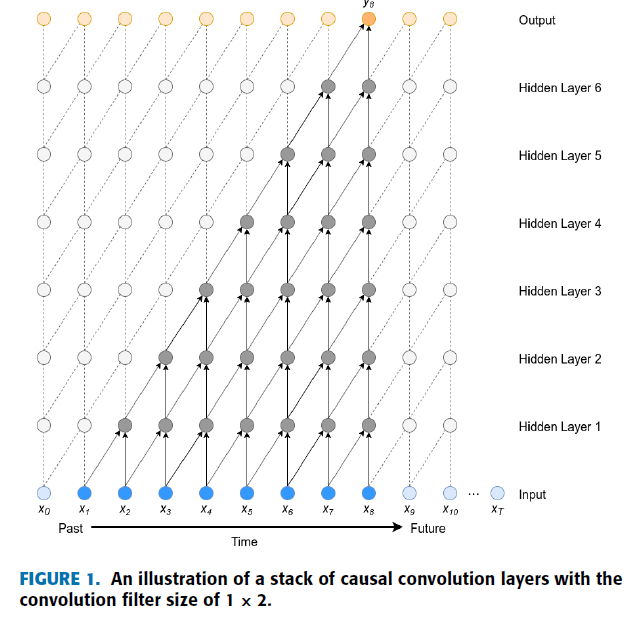
CNN을 시계열 데이터 분석에 이용하기 위해 연구자들은 Causal Convolution의 다층 구조를 이용했다. Causal Convolution이란 모델이 현재 시점까지의 데이터만을 처리하여 예측을 수행하는 것으로 아래 그림을 보면 쉽게 이해할 수 있다.

해당 그림은 참고문헌 [2]에 제시된 것으로 현재 시점의 예측인 \(y_{8}\)의 예측을 위해 \(x_{1}\)에서 \(x_{8}\) 까지의 데이터는 이용하였지만 \(x_{9}\) 부터의 데이터는 처리하지 않은 것을 보여준다. 이렇듯 예측 시점 이전까지의 데이터만을 이용하여 모델이 예측하는 Convolution 연산을 Causal Convolution이라고 한다.

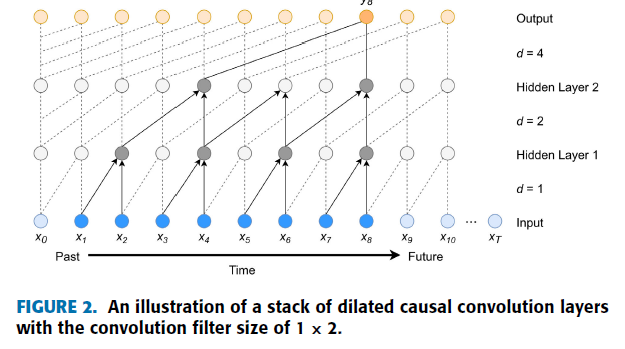
Causal Convolution은 시계열 분석에 Convolution layer을 사용가능하도록 하였지만 예측을 위해 고려할 과거 시점이 길어질수록 모델의 레이어 수를 급격히 증가시켜야 한다는 단점을 가지고 있다. 이러한 문제를 해결하기 위해 Causal Dilated Convolution이 제시되었다.

기존 Causal Convolution 기법에 Dilated Convolution 기법을 적용시켜서 Convolution layer를 깊게 쌓지 않고도 먼 과거 시점의 데이터들을 반영할 수 있게 되었다.

단일 Causal Convolutional layer에 선형 활성화 함수를 사용한 것은 auto-regressive (AR) 모델과 같다고 한다.

(ii) Recurrent Neural Networks

RNN은 과거 정보들의 요약을 포함하는 내부적인 Memory state를 포함하며, Memory state는 현재 시점에 대한 새로운 관측과 함께 회귀적으로 업데이트 된다. 이러한 정보들을 바탕으로 다음 시점의 예측을 수행하는 기법이다.

이를 수식으로 나타내면 아래와 같다.

\[\boldsymbol{z}_{t} = \nu(\boldsymbol{z}_{t-1},y_{t},\boldsymbol{x}_{t},\boldsymbol{s})\]

수식에서 \(z_{t-1}\)은 이전 시점들의 잠재 변수이고, \(y_{t}\)는 이전 관측치를 의미한다. 또한, \(\boldsymbol{x}_{t}\)와 \(\boldsymbol{s}\)는 각각 현재 입력 변수들과 메타데이터를 의미한다. \(\nu(\cdot)\)는 학습된 메모리 업데이트 함수이다.

간단한 RNN 계열의 모델 중 하나인 Elman RNN은 다음과 같은 식으로 표현할 수 있다.

\[\begin{align} y_{t+1} &= \gamma_{y}(\boldsymbol{W}_{y}\boldsymbol{z}_{t}+\boldsymbol{b}_{y}), \\ \boldsymbol{z}_{t} &= \gamma_{z}(\boldsymbol{W}_{z1}\boldsymbol{z}_{t-1} + \boldsymbol{W}_{z2}y_{t} + \boldsymbol{W}_{z3}\boldsymbol{x}_{t} + \boldsymbol{W}_{z4}\boldsymbol{s} + \boldsymbol{b}_{z}) \end{align}\]

신호 처리 관점에서는 위 Recurrent layer는 Infinite Impulse Response (IIR) 필터의 비선형 버전과 유사하다.

잠재 변수가 무한하게 과거 시점을 반영한다는 단점 때문에 기존 RNN 방법들은 데이터의 아주 오래된 시점까지 학습한다는 한계를 가지고 있다. 이를 해결하기 위해 잠재 변수를 단기 기억과 장기 기억으로 분리하는 Long Short-Term Memory Network (LSTM)이 등장했다. LSTM은 아래와 같이 입력 게이트(\(\boldsymbol{i}_{t}\)), 출력 게이트(\(\boldsymbol{o}_{t}\)), 망각 게이트(\(\boldsymbol{f}_{t}\))를 이용한다.

• Cell State: 이전 상태에서 현재 상태까지 유지되는 정보의 흐름을 나타낸다.
• Forget Gate: 이전 Cell State의 정보를 지울 것인지 말 것인지를 결정한다.

\[\begin{align} \boldsymbol{z}_{t} &= \boldsymbol{o}_{t} \odot \text{tanh}(\boldsymbol{c}_{t}), \\ \boldsymbol{c}_{t} &= \boldsymbol{f}_{t} \odot \boldsymbol{c}_{t-1} + \boldsymbol{i}_{t} \odot \text{tanh}(\boldsymbol{W}_{c1}\boldsymbol{z}_{t-1} + \boldsymbol{W}_{c2}y_{t} + \boldsymbol{W}_{c3}\boldsymbol{x}_{t} + \boldsymbol{W}_{c4}\boldsymbol{s} + \boldsymbol{b}_{c}) \end{align}\]

위 수식에서 \(\boldsymbol{f}_{t}\)가 0이라면 모델은 이전까지의 Cell State인 \(\boldsymbol{c}_{t-1}\)를 반영하지 않고 새로 입력된 \(\boldsymbol{i}_{t}\) 연산만을 반영하여 예측을 수행한다.

(iii) Attention Mechanisms

Attention layer는 동적으로 생성된 가중치들을 바탕으로 시간적인 특징들을 집계하여 네트워크가 과거의 중요한 타임 스텝에 집중할 수 있게 해준다. 개념적으로 Attention은 주어진 Query를 기반으로한 Key-Value 검색 메커니즘이며, 아래와 같은 형태를 취한다.

\[\boldsymbol{h}_{t} = \sum_{\tau=0}^{k}\alpha(\boldsymbol{\kappa}_{t}, \boldsymbol{q}_{\tau})\boldsymbol{v}_{t-\tau},\]

위 수식에서 \(\boldsymbol{\kappa}_{t}\), \(\boldsymbol{q}_{\tau}\), \(\boldsymbol{v}_{t-\tau}\)는 네트워크의 하위 단계에서 다른 타임 스텝에서 생성된 일시적인 특징을 의미한다. 또한, \(\alpha(\boldsymbol{\kappa}_{t},\boldsymbol{q}_{\tau})\in[0,1]\)은 타임 스텝 \(t\)에서 생성된 \(t-\tau\)에 대한 Attention 가중치를 의미하고 \(\boldsymbol{h}_{t}\)는 Attention layer의 Context vector를 의미한다.

시계열 모델링 관점에서 Attention은 두 가지 주요 이점을 가지고 있다. 첫 번째 이점은 Attention을 사용한 네트워크는 발생하는 어떤 주요한 사건에도 직접적으로 주의를 가질 수 있다는 점이다. 두 번째 이점은 Attention 기반의 네트워크는 각 체계별로 뚜렷한 Attention 가중치 패턴을 사용하여 체계별 시간 역학을 배울 수 있다.

(iv) Outputs and Loss Functions

신경망의 유연성을 주기 위해 심층 신경망 모델들은 Decoder를 커스터마이징하고 출력층을 원하는 타겟에 맞춤으로써 Discrete한 타겟과 Continuous한 타겟 모두를 사용한다.

\(\textbf{Point Estimates}\) 예측에서의 가장 흔한 접근은 미래에 기대되는 타겟 값을 결정하는 것이다. 이 경우는 미래의 사건을 예측하는 Discrete한 결과를 위한 분류 테스크와 연속적인 결과를 위한 회귀 테스크를 포함한다. 이 경우의 Loss Function은 다음과 같다.

\[\begin{align} \mathcal{L}_{classicification}&=-\frac{1}{T}\sum_{t=1}^{T}y_{t}\log(\hat{y}_t)+(1-y_{t})\log(1-\hat{y}_t) \\ \mathcal{L}_{regression}&=\frac{1}{T}\sum_{t=1}^{T}(y_{t}-\hat{y}_t)^2 \end{align}\]

\(\textbf{Probabilistic Outputs}\) 타겟의 미래 값을 예측하기 위해서는 Point estimates가 중요하지만, 모델 예측의 불확실성을 파악하는 것은 다양한 영역에서 의사 결정자들에게 유용할 수 있다. 예측의 불확실성을 모델링하는 일반적은 방법은 심층 신경망을 사용하여 알려진 분포의 파라미터를 도출하는 것이다. 예를 들면, 예측 분포에 대한 평균과 분산 매개변수를 심층 신경망을 통해 도출한 Gaussian Distribution이 연속 타겟에 대한 예측 문제에 일반적으로 사용되며 각 타임 스텝은 다음과 같다.

\[\begin{align} y_{t+\tau} &= N(\mu(t,\tau),\zeta(t,\tau)^2),\\ \mu(t,\tau) &= \boldsymbol{W}_{\mu}\boldsymbol{h}_{t}^{L} + \boldsymbol{b}_{\mu},\\ \zeta(t,\tau) &= \text{softplus}(\boldsymbol{W}_{\sum}\boldsymbol{h}_{t}^{L} + \boldsymbol{b}_{\sum}) \end{align}\]

\(\boldsymbol{h}_{t}^{L}\)은 네트워크의 마지막 레이어이며, \(\text{softplus}(\cdot)\)는 양의 값만을 가지기 위한 softplus 활성화 함수이다.

Softplus 활성화 함수란?

$$\text{softplus}(x)=\ln{1+e^{x}}$$ 2001년 "Incorporating Second-Order Functional Knowledge for Better Option Pricing"에서 소개된 활성화 함수로 $$x^{+}=\max(0, x)$$(RELU)의 미분가능한 버전이다.

(b) Multi-horizon Forecasting Models

통계적 관점에서 Multi-horizon Forecasting은 Single-step Forecasting을 일부 변형한 것으로 볼 수 있으며, 아래 식으로 표현할 수 있다.

\[\hat{y}_{t+\tau} = f(y_{t-k:t},\boldsymbol{x}_{t-k:t},\boldsymbol{u}_{t-k:t+\tau},\boldsymbol{s},\tau)\]

수식에서 \(\tau\in\{1,\dots,\tau_{\text{max}}\}\)는 예측 시간 스텝을 의미하며, \(\boldsymbol{u}_{t}\)는 전체 시간을 가로지르는 미래 입력, 그리고 \(\boldsymbol{x}_{t}\)는 이전에 관측된 모델 입력값을 의미한다. Multi-horizon Forecasting은 두 가지 접근법이 있는데 하나는 Iterative methods이며 하나는 Direct methods이다.

(i) Iterative Methods

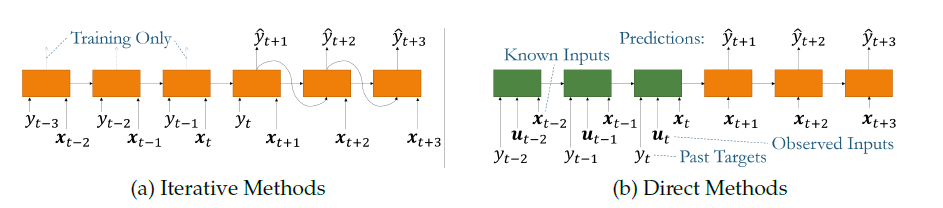
Iterative methods는 위의 그림 (a)에서 보이듯이 하나의 타임 스텝을 반복해가며 예측한다. \(t\)까지의 입력 값들을 바탕으로 \(t+1\)의 타겟 값을 예측하고, 이를 다시 입력값에 추가해서 \(t+2\)의 타겟 값을 예측한다. 하지만 각 타임 스텝에서 작은 오류들 긴 예측 구간동안 누적되어 큰 오류를 발생시킬 수 있다. 더욱이, Iterative methods는 타겟을 제외한 모든 입력 값들이 런타임 시 알려져 있다고 가정한다는 한계를 가지고 있다.

(ii) Direct Methods

Direct methods는 모든 가용 입력을 바탕으로 직접적으로 미래를 예측하기 때문에 위의 문제점들을 완화할 수 있다. 하지만 Direct methods는 사전에 정의된 이산 간격으로만 예측을 수행하기 때문에 최대 예측 길이의 지정이 필요하다.

Incorporating Domain Knowledge with Hybrid Models

Hybrid model들은 다음의 두 가지 방식으로 심층 신경망을 이용한다.

• 비확률적 모수 모델에 대한 시변 파라미터들을 인코딩
  
• 확률적 모수 모델의 분포 파라미터들을 생성

(a) Non-probabilistic Hybrid Models

모수적 시계열 모델들의 경우 예측 방정식은 일반적으로 분석적으로 정의되며 미래 목표에 대한 point 예측을 제공한다. 따라서 비확률적 Hybrid model은 이렇나 예측 방정식을 수정하여 통계 및 딥러닝 구성 요소들을 결합한다. ES-RNN (Exponential Smoothing RNN)이 Non-probabilistic Hybrid model에 속한다.

(b) Probabilistic Hybrid Models

확률적 Hybrid 모델은 분포 모델링이 중요한 응용 분야 (Gaussian process 또는 Linear state space model과 같은 시간 역학에 대한 확률적 생성 모델 등)에서 사용될 수 있다. Deep State Space Models가 Probabilistic Hybrid model에 속한다.

Facilitating Decision Support Using Deep Neural Networks

대부분의 모델 구축자들이 모델 예측의 정확도를 걱정하는 반면, 사용자들은 일반적으로 예측을 자신들의 미래 행동의 가이드로 사용한다. 따라서 시간적 역학 및 모델 예측의 동기를 더 잘 이해하는 것이 사용자가 자신의 행동을 최적화하는 데 더 도움이 될 수 있다.

(a) Interpretability With Time Series Data

신경망이 다양한 어플리케이션에 적용됨에 따라 모델이 특정 예측을 하는 방법과 이유 모두를 이해할 필요성이 증가하고 있다. 게다가 데이터 셋의 규모와 복잡성이 증가했기 때문에 사용자들은 데이터에 존재하는 관계에 대한 사전 지식을 거의 가지기 어렵다. 표준 신경망 구조의 블랙박스적 특성을 감안할 때, 딥러닝 모델을 해석하기 위한 새로운 연구 주체가 등장했다.

\(\textbf{Techniques for Post-hoc Interpretability}\) 사후 해석 모델은 학습된 네트워크의 해석을 위해 개발되었으며 기존 가중치를 수정하지 않고도 중요한 특징이나 예시를 식별할 수 있도록 도와준다. 사후 해석 모델은 두 가지 접근법으로 나뉘는데 첫 번째는 신경망의 입력과 출력 사이에 더 단순한 해석가능한 surrogate model을 적용하고 근사된 모델을 기반으로 해석을 제공하는 것이다. Local Interpretable Model-Agnostic Explanations (LIME)과 Shapley additive explanations (SHAP)가 해당 접근법에 속한다. 두 번째는 어떠한 입력 특징이 손실 함수에 가장 큰 영향을 미치는지 결정하기 위해 신경망의 그레디언트를 분석하는 그레디언트 기반 방법이다. Saliency maps와 influence function이 이 접근법에 속한다.

\(\textbf{Inherent Interpretability with Attentions Weights}\) 대안적 접근법은 전략적으로 배치된 Attention layer의 형태로 설명 가능한 구성요소를 가진 네트워크 구조를 직접 설계하는 것이다. Attention 가중치의 분석은 각 타임 스텝에서 특징간 상대적 중요도를 이해하는데 사용될 수 있다.

(b) Counterfactual Predictions & Causal Inference Over Time

Coutfactual predictions은 사용자가 다양한 행동에 따라 목표 궤적에 어떻게 영향을 미치는지 평가할 수 있다는 관점에서 시나리오 분석 어플리케이션에서 특히 유용하다. 이는 다른 상황이 발생했다면 어떻게 되었을지를 결정하는 역사적 관점과 미래 결과를 최적화 하기 위해 어떤 조취를 취할 것인지를 결정하는 예측 관점 모두에서 유용할 수 있다.

정적인 설정에서 인과 효과를 추정 하기 위한 많은 종류의 딥러닝 방법이 존재하지만, 시계열 데이터 셋의 핵심 과제는 시간 의존적 교란 효과의 존재이다. 이것은 타겟에 영향을 미칠 수 있는 행위가 타겟에 대한 관찰을 조건으로 하는 경우 순환 의존성으로 인해 발생한다. 시간 의존적 교란의 보정이 없는 간단한 추정 기법의 경우에는 편향된 결과를 가질 수 있다. 최근 통계적 기술의 확장과 새로운 손실 함수의 설계를 기반으로 시간 의존적 교란을 보정하며 심층 신경망을 학습시키기 위한 연구가 진행되고 있다.

Conclusions and Future Directions

• 심층 신경망은 일반적으로 시계열을 일정한 간격으로 이산화해야하기 때문에 관측치가 누락되거나 임의의 간격으로 도착할 수 있는 데이터 셋을 예측하는데 어려움이 있다. 그러므로 복잡한 입력을 활용할 수 있도록 추가적인 연구가 필요하다.
• 신경망은 종종 궤적 간의 논리적 그룹을 갖는 계층적 구조를 가진다. 이러한 계층 구조를 명시적으로 설명하는 구조의 개발은 흥미로운 연구 방향이 될 수 있으며, 잠재적으로 기존의 일변량 또는 다변량 모델보다 예측 성능을 향상시킬 수 있다.

References

1. Lim, Bryan, and Stefan Zohren. “Time-series forecasting with deep learning: a survey.” Philosophical Transactions of the Royal Society A 379.2194 (2021): 20200209.
2. Duc, Tho Nguyen, et al. “Convolutional neural networks for continuous QoE prediction in video treaming services.” IEEE Access 8 (2020): 116268-116278.
3. Dugas, Charles, et al. “Incorporating second-order functional knowledge for better option pricing.” Advances in neural information processing systems 13 (2000).