[Paper Review] SegRNN: Segment Recurrent Neural Network for Long-Term Time Series Forecasting

Paper Information

Title: SegRNN: Segment Recurrent Neural Network for Long-Term Time Series Forecasting Authors: Shengsheng Lin, Weiwei Lin et al. Link: https://arxiv.org/abs/2308.11200

Summary

• 저자들은 예측해야할 시퀀스의 길이가 증가함에 따라 RNN의 반복적인 회귀 횟수가 급격히 증가하는 문제로 인해 Long-term Time Series Forecasting 분야에서 성공하지 못했다고 분석하였습니다.
• 이러한 문제를 해결하기 위해 Segment-wise iteration 기법과 Parallel Multi-step Forecasting 전략을 제시하였으며, 이를 통해 추론 시간을 감소시키며 예측 성능을 향상시켰습니다.

Introduction

• Long-term Time Series Forecasting (LTSF) 분야에서 Recurrent Neural Network (RNN) 기반의 방법들은 긴 look-back window와 forecast horizon을 처리하는 것에 어려움이 있습니다.
• 저자들은 LTSF 분야에서 RNN은 극도로 긴 look-back window와 forecast horizon으로 인해 발생하는 엄청나게 높은 반복 횟수로 인해 실패했다고 분석했습니다.
• 이를 해결하기 위해 저자들은 (1) point-wise iteration을 segment-wise iteration으로 대체하였으며, (2) Parallel Multi-step Forecasting (PMF) 전략을 제시하였습니다.

Preliminaries

LTSF Problem Formulation

LTSF는 다변량 과거 시계열 \(X \in \textbf{R}^{L \times C}\)를 입력받아 미래 시계열 \(Y \in \textbf{R}^{H \times C}\)를 예측하는 문제입니다. 수식에서 \(L\), \(C\), 그리고 \(H\)는 각각 과거의 look-back window의 길이, 특징의 차원이나 채널의 수, 그리고 forecast horizon의 길이를 의미합니다.

Channel Independent Strategy

Channel Independent (CI) Strategy는 (Han, Ye, and Zhan 2023)이 제안한 방법으로 다변량 과거 시계열 데이터를 미래 시계열 값에 매핑하는 \(f: X \in \textbf{R}^{L \times C} \rightarrow Y \in \textbf{R}^{H \times C}\)와 달리 일변량 과것 ㅣ계열 데이터를 미래 시계열 값에 매핑하는 함수 \(f: X^{(i)} \in \textbf{R}^{L} \rightarrow Y^{(i)} \in \textbf{R}^{H}\)를 식별하는 것을 목표로 하고 있습니다.

Model Architecture

RNN의 반복적인 회귀특성은 광범위한 시퀀스를 모델링할 때 효과적으로 수렴하기 위한 도전에 직면해 있습니다. SegRNN은 모델의 수렴을 위해 반복적인 회귀를 줄이는 것을 목표로 하였으며 아래의 전략들을 채택하였습니다.

• 인코딩 페이즈에서 point-wise iteration을 segment-wise iteration으로 대체하였으며, 반복의 횟수를 \(L\)에서 \(L/w\)로 감소시켰습니다. (\(w\)는 segment의 길이)
• 디코딩 페이즈에서 PMF 전략을 채택하였으며, 반복의 횟수를 \(H/w\)에서 \(1\)로 감소시켰습니다.

본 논문의 저자들이 제안한 SegRNN의 아키텍처는 아래 그림과 같습니다.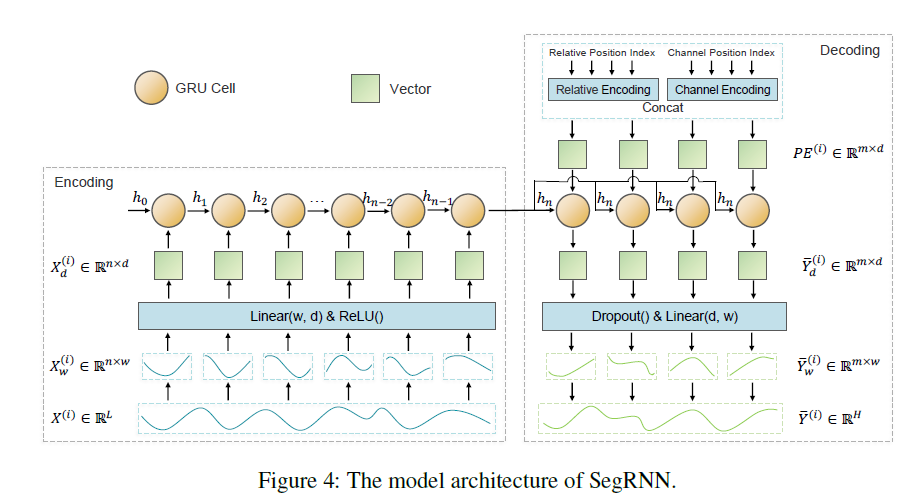

Encoding

\(\textbf{Segment partition and projeection}\)

• 주어진 입력 \(X^{(i)} \in \textbf{R}^{L}\)를 segment \(X_{w}^{(i)} \in \textbf{R}^{n \times w}\)로 분할합니다. (수식에서 \(w\)는 segment의 길이이며 \(n\)은 segment의 개수)
• 분할된 segment \(X_{w}^{(i)} \in \textbf{R}^{n \times w}\)들은 학습가능한 선형 투사 \(W_{prj} \in \textbf{R}^{w \times d}\)와 활성화 함수 ReLU를 거쳐 \(X_{d}^{(i)} \in \textbf{R}^{n \times d}\)로 변형됩니다.

\(\textbf{Recursive encoding}\)

• 변형된 \(X_{d}^{(i)}\)들은 시간적 특징을 포착하기 위한 반복적인 회귀를 위해 GRU에 입력으로 주어집니다.
• 구체적으로 GRU cell에서 \(X_{d}^{(i)}\)의 요소 \(x_{t} \in \textbf{R}^{d}\)가 거치는 프로세스를 수식화하면 다음과 같습니다.

\[\begin{align} z_{t} &= \sigma (W_{z} \cdot [h_{t-1},x_{t}]),\\ r_{t} &= \sigma (W_{r} \cdot [h_{t-1},x_{t}]),\\ \tilde{h}_{t} &= \tanh (W \cdot [r_{t} \times h_{t-1},x_{t}]),\\ h_{t} &= (1 - z_{t}) \times h_{t-1} + z_{t} \times \tilde{h}_{t} \end{align}\]

\(n\)번의 반복이 끝난 후에 얻어지는 \(h_{n}\)은 기존의 시퀀스 \(X^{i}\)의 모든 시간적인 특징을 캡슐화합니다.

Decoding

Recurrent Multi-step Forecasting (RMF)는 single-step prediction을 반복적으로 수행하는 방법으로 예측된 \(\bar{y}_{t}\)는 다음 값인 \(\bar{y}_{t+1}\)의 예측을 위해 입력으로 사용되며, 이러한 프로세스를 반복적으로 수행하는 방법입니다. 인코딩 페이즈에서 segment 기법을 적용하였으므로 \(H\) horizon을 예측하기 위한 반복은 \(H/w\)로 감소되었습니다.

반복적인 회귀 횟수의 감소에도 불구하고 반복적인 디코딩은 다음과 같은 한계점들을 가지고 있습니다.

• 반복적인 예측으로부터 발생하는 에러의 누적
• 병렬 연산을 방해하며 추론 속도의 향상을 제한시키는 회귀 특성

이러한 한계점들을 해결하기 위해 저자들은 Parallel Multi-step Forecasting (PMF) 전략을 제안하였습니다.

\(\textbf{Positional embeddings}\)

• 디코딩 페이즈를 거치는 동안 반복적인 회귀로 인해 segment들의 순서 정보가 손실되는 경우가 발생합니다.
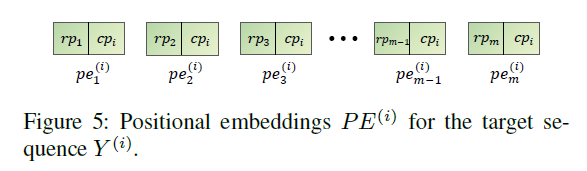
• 저자들은 Positional embeddings \(PE^{i} \in \textbf{R}^{m \times d}\)를 통해 각 segment들의 위치 정보를 제공합니다.
• 각각의 \(pe^{i} \in \textbf{R}^{d}\)는 상대적 위치 인코딩 \(rp \in \textbf{R}^{\frac{d}{2}}\)와 채널 위치 인코딩 \(cp \in \textbf{R}^{\frac{d}{2}}\)로 구성됩니다.

• 저자들은 채널 위치 인코딩을 포함하는 것은 변수들 사이의 관계들을 포착하는 것에 있어서 CI 전략의 한계들을 부분적으로 보상해준다고 설명하고 있습니다.

\(\textbf{Parallel decoding}\)

• 인코딩 페이즈에서 생성된 \(h_{n}\)을 \(m\)번 복제하고 Positional embedding \(PE^{i}\)와 결합하여 병렬적으로 GRU 셀에 입력합니다.
• 병렬 연산을 거치면 길이가 \(d\)인 \(m\)개의 벡터들, \(\bar{Y}_{d}^{(i)} \in \textbf{R}^{m \times d}\)가 생성됩니다.
• 미래의 값들을 순차적으로 생성하지 않고 병렬적으로 생성하는 방법이 저자들이 채택한 PMF 전략입니다.

\(\textbf{Prediction and sequence recovery}\)

• 앞선 단계에서 생성된 \(\bar{Y}_{d}^{(i)}\)는 선형 함수와 Dropout을 거쳐 \(\bar{Y}_{w}^{(i)}\)로 변환되며, segment들을 합쳐서 최종 예측인 \(\bar{Y}^{(i)} \in \textbf{R}^{H}\)가 됩니다.

Normalization and Evaluation

\(\textbf{Instance normalization}\)

• 저자들은 입력된 시퀀스의 마지막 값을 빼주는 방식의 간단한 normalization 방법을 채택하였으며, 수식은 아래와 같습니다.

\[\begin{align} x_{1:L}^{(i)} &= x_{1:L}^{(i)} - x_{L}^{(i)},\\ \bar{y}_{1:L}^{(i)} &= \bar{y}_{1:L}^{(i)} + x_{L}^{(i)} \end{align}\]

\(\textbf{Loss function}\)

• SegRNN은 mean absolute error (MAE)를 loss function으로 채택하였으며, 수식은 아래와 같습니다.

\[\mathcal{L}(Y,\bar{Y}) = \frac{1}{HC}\sum^{H}_{t=1}{\sum^{C}_{i=1}{|\bar{y}_{t}^{(i)}-y_{t}^{(i)}|}}\]